Graphs
A graph is a data structure that consists of a finite set of vertices (or nodes) and a collection of edges connecting these vertices. The edges may or may not have a direction, and they may have weights or labels. Graphs are used to represent relationships and connections between different entities.
Components of a Graph:
- Vertices (Nodes):
- The fundamental entities in a graph.
- Represented by points in a graph.
- Edges:
- Connections between vertices that represent relationships.
- An edge can be directed (arrow indicating a one-way connection) or undirected (no direction).
Types of Graphs:
- Directed Graph (DiGraph):
- Edges have a direction, indicating a one-way connection.
- Undirected Graph:
- Edges have no direction; connections are bidirectional.
- Weighted Graph:
- Edges have weights or costs assigned to them.
- Cyclic Graph:
- Contains at least one cycle (a path that starts and ends at the same vertex).
- Acyclic Graph:
- Does not contain any cycles.
- Connected Graph:
- There is a path between every pair of vertices.
- Disconnected Graph:
- Contains at least two vertices with no path between them.
Graph Representation:
- Adjacency Matrix:
- A 2D array where the entry
matrix[i][j]represents whether there is an edge between verticesiandj.
- A 2D array where the entry
Graph Operations:
- Add Vertex and Edge:
- Adding new vertices and connecting them with edges.
- Remove Vertex and Edge:
- Removing vertices and edges from the graph.
- Traversal:
- Visiting all vertices and edges in the graph following a specific order.
- Common traversal algorithms include Depth-First Search (DFS) and Breadth-First Search (BFS).
Applications of Graphs:
- Networks:
- Modeling social networks, computer networks, transportation networks.
- Routing Algorithms:
- Finding the shortest path between two vertices.
- Dependency Analysis:
- Analyzing dependencies between different components.
- Circuit Design:
- Representing connections in electronic circuits.
- Recommendation Systems:
- Providing recommendations based on connections in user data.
Graph Traversal Techniques:
Breadth-First Search (BFS):
- Description:
- BFS explores all the vertices at the current level before moving on to the next level.
- Uses a queue to maintain the order of vertex exploration.
- Algorithm:
- Start at a source vertex and mark it as visited.
- Enqueue the source vertex.
- Dequeue a vertex and visit its unvisited neighbors.
- Enqueue unvisited neighbors.
- Repeat steps 3-4 until the queue is empty.
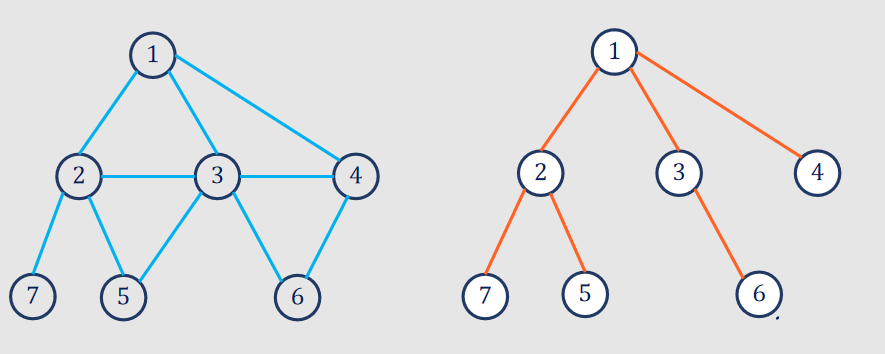
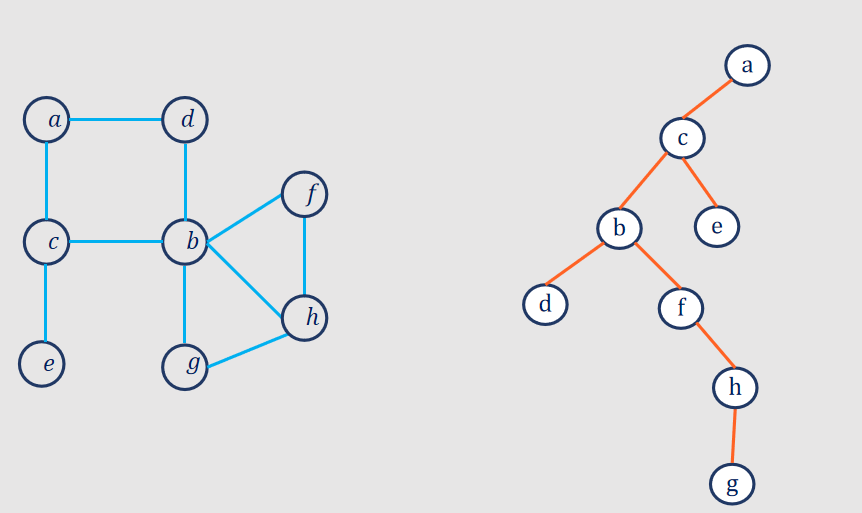
Depth-First Search (DFS):
- Description:
- DFS explores as far as possible along each branch before backtracking.
- Uses a stack (either explicitly or through recursion) to keep track of vertices.
- Algorithm:
- Start at a source vertex and mark it as visited.
- Explore an unvisited neighbor of the current vertex.
- If no unvisited neighbor, backtrack to the previous vertex.
- Repeat steps 2-3 until all vertices are visited.
Minimum Spanning Tree (MST):
A Minimum Spanning Tree (MST) of a connected, undirected graph is a tree that spans all the vertices of the graph and has the minimum possible total edge weight. In other words, it is a subset of the edges of the graph that forms a tree and connects all the vertices with the minimum total edge weight.
Key properties of a minimum spanning tree:
- Connectivity: It connects all the vertices in the original graph.
- Acyclic: It forms a tree, meaning there are no cycles in the tree.
- Minimum Weight: The sum of the edge weights in the tree is minimized.
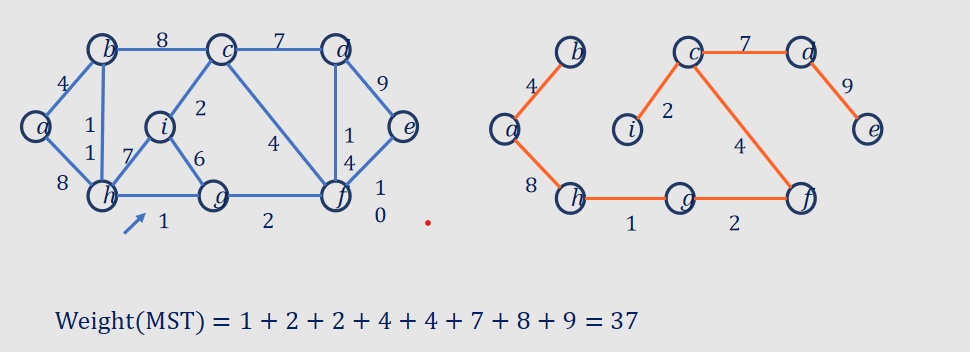
1. Kruskal's Algorithm:
- Algorithm Steps:
- Initialize the MST as an empty set.
- Sort all the edges in non-decreasing order of their weights.
- Iterate through the sorted edges and add each edge to the MST if it does not form a cycle.
- Stop when the MST contains (V-1) edges, where V is the number of vertices.
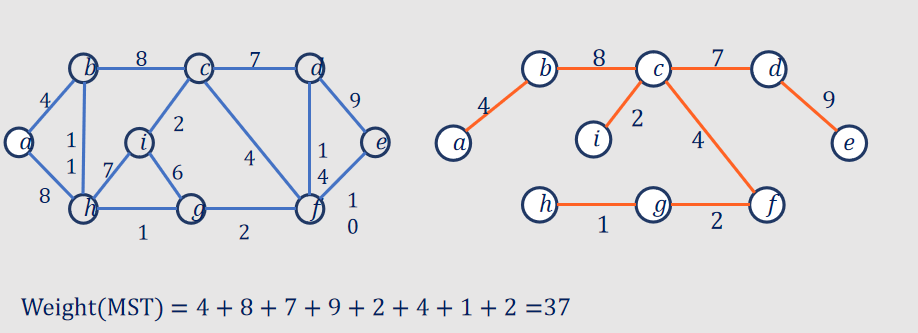
2. Prim's Algorithm:
- Algorithm Steps:
- Start with an arbitrary vertex as the initial MST.
- At each step, add the minimum weight edge that connects a vertex in the MST to a vertex outside the MST.
- Repeat until all vertices are included in the MST.
Difference Between BFS and DFS:
| Feature | Breadth-First Search (BFS) | Depth-First Search (DFS) |
| Exploration Order | Visits all neighbors at the current level before moving on to the next level. | Explores as far as possible along each branch before backtracking. |
| Data Structure Used | Uses a queue to maintain the order of vertex exploration. | Uses a stack (either explicitly or through recursion) to keep track of vertices. |
| Application | Often used for finding the shortest path in unweighted graphs. | Commonly used for detecting cycles, topological sorting, and solving maze problems. |
| Completeness | Guarantees the shortest path in unweighted graphs. | Does not guarantee the shortest path. |
| Order of Exploration | Explores vertices in the order they are enqueued. | Explores vertices in the order they are popped from the stack. |
| Example Use Case | Finding the shortest path between two nodes in an unweighted graph. | Detecting cycles in a graph or performing topological sorting. |
Difference Between Kruskal’s and Prism’s:
| Feature | Kruskal's Algorithm | Prim's Algorithm |
| Algorithm Type | Greedy algorithm that selects edges based on weight without forming cycles. | Greedy algorithm that grows the tree from an initial vertex. |
| Operation | Works by repeatedly adding the smallest edge that doesn't form a cycle. | Works by growing the tree from an initial vertex, adding the smallest edge to connect the tree with the rest of the graph. |
| Edge Selection | Chooses edges based on weight without concern for the source or destination vertices. | Chooses edges based on weight to connect the current tree with the closest non-tree vertex. |
| Deterministic Output | May have multiple valid solutions depending on the order edges are considered. | Always produces the same minimum spanning tree for a given starting vertex. |
| Use Cases | Suitable for sparse graphs and scenarios where edge weights are relatively uniform. | Suitable for dense graphs and scenarios where there is a clear central location or starting vertex. |