Trees

Binary Tree:

A Binary tree is a hierarchical data structure in which each node has at most two children, referred to as the left child and the right child. The topmost node in a binary tree is called the root, and nodes with no children are called leaves.

Binary Search Tree:

A Binary Search Tree (BST) is a type of binary tree with the additional property that the value of each node is greater than or equal to the values of all nodes in its left subtree and less than or equal to the values of all nodes in its right subtree. This key property makes binary search trees particularly useful for efficient searching and retrieval of data.

Operations of Binary Search Tree:

1. Insertion:

   Inserting a new node into the binary tree.

   • Procedure:
     • Compare the value to be inserted with the root node.
     • If the value is smaller, move to the left subtree; if larger, move to the right subtree.
     • Repeat the process until an empty spot is found, then insert the new node.

2. Deletion:

   Removing a node from the binary tree.

   • Procedure:
     • Locate the node to be deleted.
     • Handle different cases:
       1. If the node has no children, simply remove it.
       2. If the node has one child, replace it with its child.
       3. If a node has two children:
          • Find the node with the next larger value (in-order successor) or the next smaller value (in-order predecessor).
          • Replace the value of the current node with the value of the found node.
          • Delete the node found in step 1.
            • This replacement node will have either no children or only a right (or left) child

3. Search (Traversal):

   Traversing the binary tree to find a specific node.

   • Procedures:
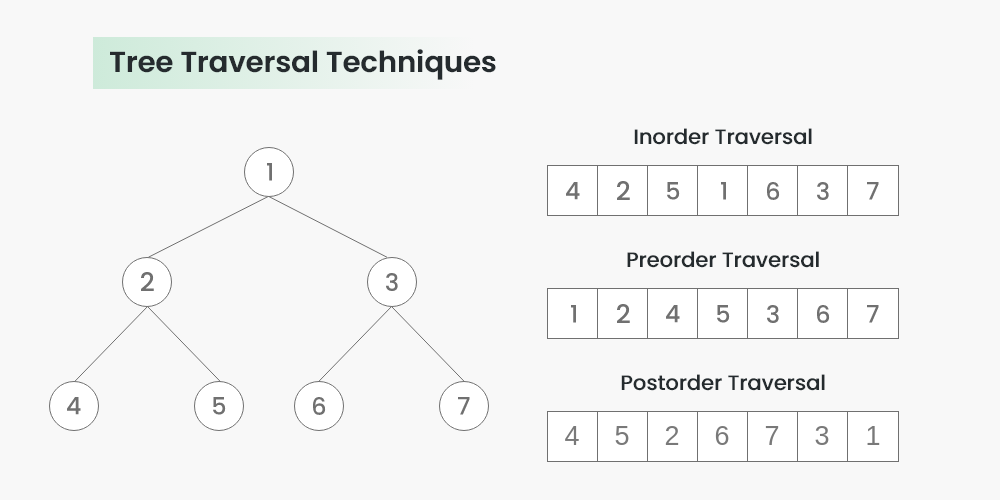
     • In-Order Traversal: Visit left subtree, visit the current node, visit right subtree.
     • Pre-Order Traversal: Visit the current node, visit left subtree, visit right subtree.
     • Post-Order Traversal: Visit left subtree, visit right subtree, visit the current node.

4. Search (Lookup):

   Locating a specific value in the binary tree.

   • Procedure:
     • Compare the value to be found with the value of the current node.
     • If equal, the node is found.
     • If smaller, move to the left subtree; if larger, move to the right subtree.
     • Repeat until the node is found or a null pointer is reached.

5. Minimum and Maximum:

   Finding the node with the smallest or largest value in the binary tree.

   • Procedures:
     • Minimum: Traverse to the leftmost node of the tree.
     • Maximum: Traverse to the rightmost node of the tree.

6. Height (or Depth):

   Determining the height or depth of the binary tree.

   • Procedure:
     • Recursively calculate the height of the left and right subtrees, and return the maximum plus one.

Properties of a Binary Tree:

1. Root:
   • The topmost node in the tree, from which all other nodes are descended.

2. Node:
   • Each element in the binary tree is called a node, containing a key, and optionally, left and right children.

3. Parent and Children:
   • A node in a binary tree is considered the parent of its left and right children.

4. Leaf:
   • A node with no children is called a leaf or a terminal node.

5. Subtree:
   • A subtree is a tree formed by a node and its descendants.

6. Depth:
   • The depth of a node is the number of edges on the path from the root to that node.

7. Height:
   • The height of a binary tree is the length of the longest path from the root to a leaf. It is the number of edges on the longest path from the root node to a leaf node.

8. Binary Tree Levels:
   • The levels of a binary tree are numbered starting from the root, with the root at level 0.

9. Balanced vs. Unbalanced:
   • A balanced binary tree is one in which the height of the left and right subtrees of any node differs by at most one.
   • An unbalanced binary tree may have significant differences in the heights of its left and right subtrees.

Memory Representation:

The memory representation of a binary tree involves allocating memory for each node and establishing links between nodes using pointers.

• Each node contains a key or value.

• The left child pointer points to the left child node.

• The right child pointer points to the right child node.

Applications of Trees:

• Binary Search Trees (BST):
  • Search and Retrieval

• Heap Data Structure:
  • Priority Queues

• Expression Trees:
  • Mathematical Expressions

• File System:
  • Directory Structures

• HTML DOM (Document Object Model):
  • Web Page Structure

• Networking:
  • Routing Tables

• Database Systems:
  • Indexing

• Compiler Design:
  • Abstract Syntax Trees (AST)

• Artificial Intelligence and Machine Learning:
  • Decision Trees

• Graph Algorithms:
  • Spanning Trees